Fly me to the Alpha Centauri
https://www.acmicpc.net/problem/1011
1011번: Fly me to the Alpha Centauri
우현이는 어린 시절, 지구 외의 다른 행성에서도 인류들이 살아갈 수 있는 미래가 오리라 믿었다. 그리고 그가 지구라는 세상에 발을 내려 놓은 지 23년이 지난 지금, 세계 최연소 ASNA 우주 비행
www.acmicpc.net
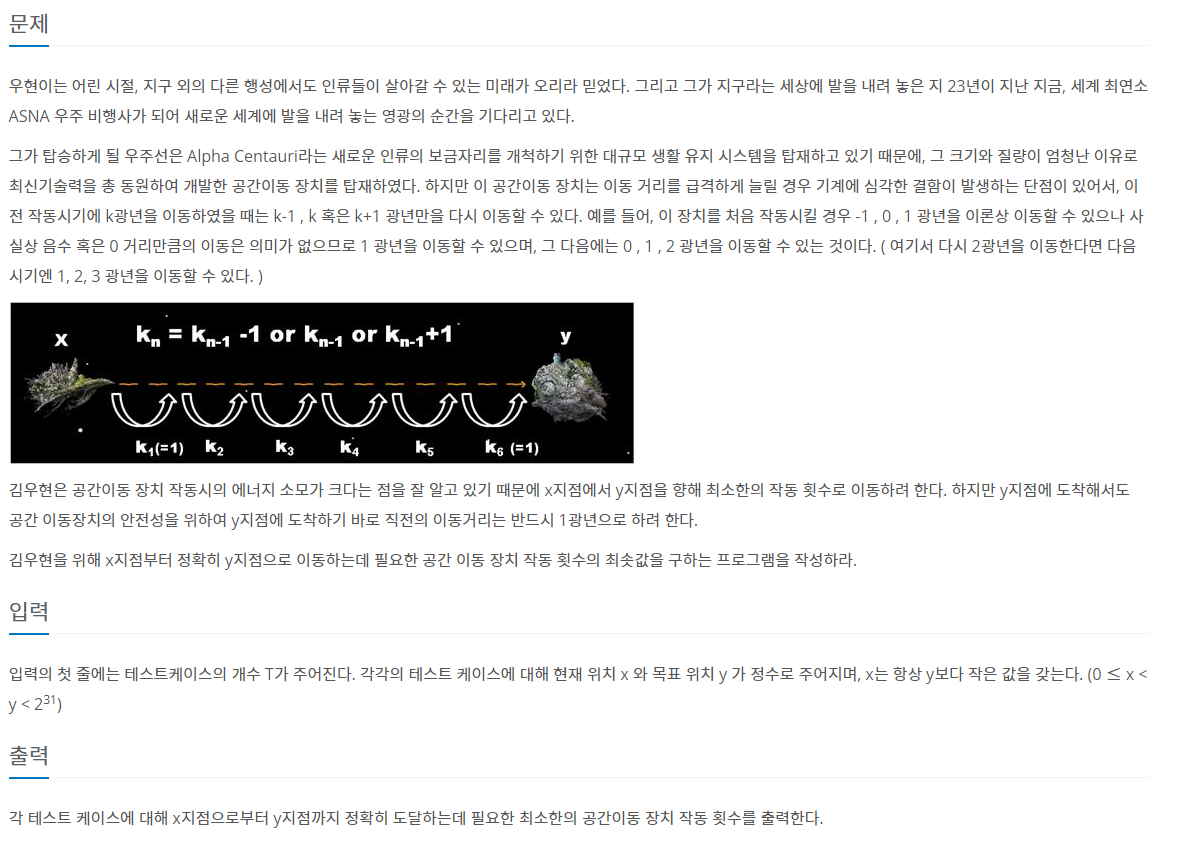
이동 거리가 계속 변하는 경우라서 어떻게 계산해야 될지 고민했다.
마지막 Y지점에 도착할 때 바로 직전의 이동거리는 1광년이 되어야 한다. 그러기 위해서는 그 전에는 2광년, 또 그 전에는 3광년으로 순차적으로 줄어들어야 한다.
가장 적은 횟수로 이동하기 위해서는 최대로 많이 움직일 수 있는 거리인 k광년에 도달했다가 다시 1광년 거리를 이동하는 경우이다.

이 경우 이동한 거리는 1+2+3+...+k+...+3+2+1 = k*k로 계산할 수 있다.
이동해야할 거리를 k*k로 표현할 수 있다면 이동한 횟수는 k + (k-1) = 2k - 1 이 된다.
만약 k*k보다 크고 (k+1)*(k+1) 작다면 어떻게 계산할 수 있을까?
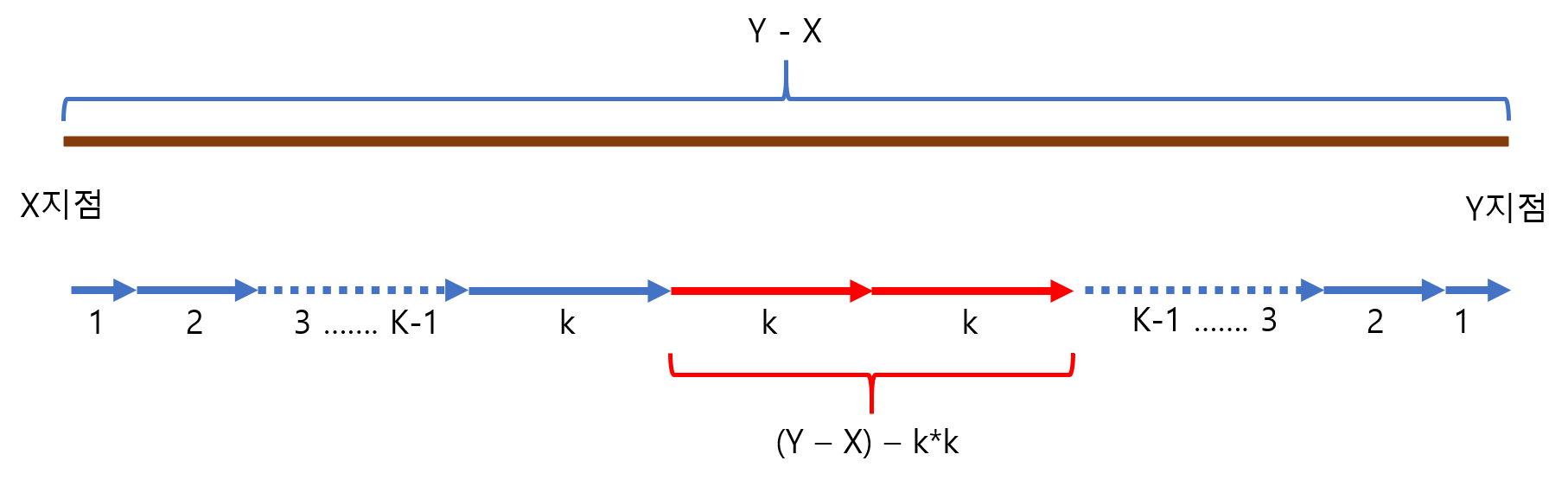
k*k만큼 이동하고 부족한 거리를 k광년씩 최대한 이동하는 것이 좋다.
k만큼 여러번 이동했는데도 남는 거리가 있다면 중간에 그만큼 한번 이동해주면 된다.(어쨌든 k보다 작은 거리이기 때문)
코드를 작성해보면 다음과 같다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
|
T = int(input())
for _ in range(T):
x, y = map(int, input().split())
d = y - x
k = 1
while True:
if (k * k) <= d and d < (k+1)*(k+1): break
else: k += 1
if (d - (k * k)) % k == 0:
plus = (d - (k * k)) // k
else:
plus = (d - (k * k)) // k + 1
print(2*k -1 + plus)
|
cs |
한 번에 최대한 이동할 수 있는 거리인 k광년을 구하고, 남는 거리를 k로 나눴을때 나머지가 있는지 확인한다.
있으면 +1번, 없으면 남는거리를 k로 나눈 횟수만큼 더해주면 된다.
'알고리즘' 카테고리의 다른 글
| 백준 - 2581번, 1929번 / 소수 (0) | 2021.08.05 |
|---|---|
| 백준 - 1978번 / 소수 (0) | 2021.08.04 |
| 백준 - 2775번 / 함수의 호출 횟수(counter) (0) | 2021.08.03 |
| 백준 - 10250번 (0) | 2021.08.03 |
| 백준 - 2869번 (0) | 2021.08.03 |